Kröger–Vink notation

Kröger–Vink notation is set of conventions used to describe electric charge and lattice position for point defect species in crystals. It is primarily used for ionic crystals and is particularly useful for describing various defect reactions. It was proposed by F. A. Kröger and H. J. Vink.^[1]^[2]

General format

$M^C_S$

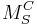
M corresponds to the species. These can be

atoms – e.g., Si, Ni, O, Cl,
vacancies – V or v (since V is also the symbol for vanadium)
electrons – e
electron holes – h

S indicates the lattice site that the species occupies. For instance, Ni might occupy a Cu site. In this case, M would be replaced by Ni and S would be replaced by Cu. The site may also be a lattice interstice. In this case the symbol 'i' is used.

C corresponds to the electronic charge of the species relative to the site that it occupies. To continue the previous example, Ni often has the same valency as Cu, so the relative charge is zero. To indicate null charge, × is used. A single • indicates a single positive charge, while two would represent two positive charges. Finally, ′ signifies a single negative charge, so two would indicate a double negative charge.

Examples

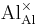$\mathrm{Al}^\times_\mathrm{Al}$ = an aluminum ion sitting on an aluminum lattice site, with neutral charge.

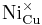$\mathrm{Ni}^\times_\mathrm{Cu}$ = a nickel ion sitting on a copper lattice site, with neutral charge.

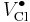${V}^{\bullet}_\mathrm{Cl}$ = a chlorine vacancy, with singular positive charge.

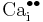$\mathrm{Ca}^{\bullet\bullet}_\mathrm{i}$ = a calcium interstitial ion, with double positive charge.

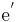$\mathrm{e}^{'}_{}$ = an electron. A site isn't normally specified.

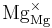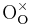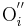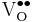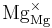$\mathrm{Mg}^\times_\mathrm{Mg}$ + $\mathrm{O}^\times_\mathrm{O}$ → $\mathrm{O}^{''}_i$ + $\mathrm{V}^{\bullet\bullet}_\mathrm{O}$ + $\mathrm{Mg}^\times_\mathrm{Mg}$ = A Kröger-Vink representation of Frenkel defect formation in MgO.

The following are the chemical equations in Kröger–Vink notation for the formation of Schottky defects in TiO₂ and BaTiO₃.

Ø 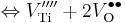$\Leftrightarrow V_\mathrm{Ti}'''' %2B 2V_\mathrm{O}^{\bullet \bullet}$

Ø 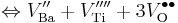$\Leftrightarrow V_\mathrm{Ba}'' %2B V_\mathrm{Ti}'''' %2B 3V_\mathrm{O}^{\bullet \bullet}$

References

^ F.A. Kröger and H.J. Vink, in Solid State Physics, vol. 3, editors: F. Seitz, D. Turnbull, p. 273–301, (1956)
^ C. Barry Carter and M. Grant Norton, Ceramic Materials: Science and Engineering, Springer, New York (2007) ISBN 0387462708